Today I was meant to be writing up journal entries and getting ready for school tomorrow, as well as finishing attaching the strings to the parachute that I still haven’t done and start making the box which the camera needs to go in for a second launch on Wednesday or Thursday and hack one of the cameras and do a battery test and and and… Sigh. Okay, rant over.
Okay, so I had a lot of stuff that I needed to do today, and as usual, when the stress piles on too high, I find the most random and unrelated thing that I can, and give my undivided attention to that for as long as possible. It’s not a very good habit, but since I have it, I tend to make the most of it.
Before I start describing in intense detail what I didn’t do, perhaps I should start with the one thing I did. Well, I didn’t actually do it but that’s not the point. Michael replied to my email with the gazillion questions I had, and gave the go-ahead to use Intermet’s internet (J) for our tracker 2.0. On the down side, he told me that they only work four days a week from Monday to Thursday, meaning I wouldn’t be able to launch on a Saturday. Another bummer was that from next week on, they will be doing three dual soundings per day as part of their product testing, so he doesn’t think they’ll be able to fit in any additional launches for me. I will have to actually get hold of Rian soon, as I may be needing him again very soon…
Michael also told me that the earliest they are allowed to launch is 7:30 in the morning, so I’ll have to find another place to launch if I want to get a Golden Hour sunrise. This is where the day’s procrastination events came into play, as I got thinking about how to calculate the time of Golden Hour, based on the height and location of the balloon. This is what I came up with:
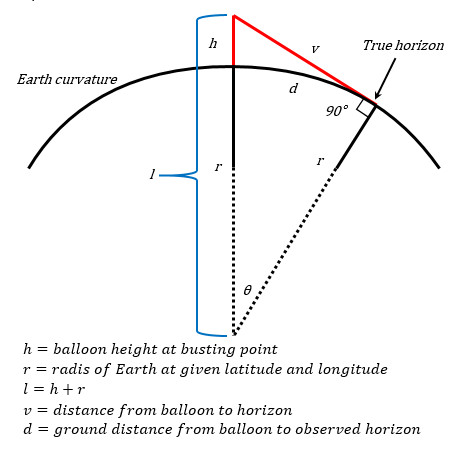
Firstly, the height of the balloon at bursting point is needed, as it is at this point that it’s the most stable, meaning the best photos. Since there is no way to measure how much Hydrogen gas gets pumped into the balloon at launch, it is difficult to predict at what altitude it till burst. However, it is safe to assume that it can be anywhere from 25 000m to 35 000m. A mathematical notation for this would be:
![]()
Next, the radius of the earth needs to be calculated. According to Google, the radius of Earth is 6 371km. However that is the mean radius. The earth is not a true sphere. It is an “Oblate Spheroid”. This is due to the angular velocity of earth rotating about its minor axis. The momentum expands the equator of the planet ever-so-slightly, turning it into a spheroid. This effect is also enough to flatten the poles slightly, making the earth an oblate spheroid. Due to the bulge at the equator, the equatorial and polar radii differ slightly. The equatorial radius is 6 378.137km, while the polar radius is 6 356.7523km.
Contextually the difference is not that great being about 20km, however since that is two thirds the height that my balloon will travel vertically, I think it necessary to make sure there is as little error as possible. The formula I derived was rather simple: take the minimum radius value (the polar radius) and from it subtract the subtraction of the minimum radius (polar) from the maximum radius (equatorial) divided by ninety degrees (as there are ninety degrees from the equator to the poles along the lines of latitude) times by the balloon bursting latitude location. Mathematically, the notation looks as follows:

I know that roughly all of the balloons burst around 34°12’00”S (-34.2° in decimal form), so I plugged that latitude into the equation and calculations were simple from there:
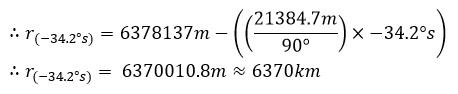
The radius of Earth at -34.2° turned out to be 1km less than the mean radius, so not much difference (but will still increase accuracy)
Next I had to calculate the distance of the center of the earth to the weather balloon at bursting altitude. As I already knew the distance of the center of the earth to the surface and from there to the weather balloon’s variable bursting altitudes, it was simple addition to work out the final values:
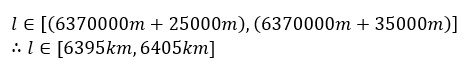
Although this next step was not crucial to working out Golden Hour, it was interesting to work out. In order to calculate the distance from the balloon at bursting altitude to the horizon I had to use the Pythagorean Theorem. This took a while to figure out, as I had to remember the rules with tangents on a circle. Eventually I wrapped my head around it:
“Imagine a line running vertically from the balloon to the center of the earth, call it line ‘l’. ‘l’ is just the height of the balloon plus the radius of the earth. Now imagine running a line from the top of the vertical line (where the balloon is), to the edge of the circle until it touches. Now keep extending that line so that it becomes tangent to the circle. Next, where the line touches the circle draw a perpendicular line extending to the center of the earth until it touches the bottom of the vertical line ‘l’. Now there is a triangle with a right angle. Imagine line ‘l’ is the hypotenuse, the radius (perpendicular line) is called ‘r’ and the distance from the top of line ‘l’ (where the balloon is) to where the line meets the circle at a tangent is called ‘v’. Since we know the length of ‘l’ and the length of ‘r’, calculating the value of ‘v’ is simple using the Pythagorean Theorem.
Mathematically it would look something like this:
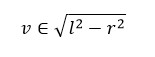
Since we calculated ‘l’ to be an element of 6 395km and 6 405km, and ‘r’ to be approximately 6 370km, we can say with certainty that:

With that out of the way it was time for the fun part. In order to calculate the actual ground distance of the location of the weather balloon to the observed horizon line from its bursting altitude, the circumference of the earth needed to be calculated, then divided by 360°, then multiplied by the angle between the balloon bursting location and the observed horizon location. Since working out the circumference of the earth was easy thanks to the formula “circumference is equal to two Pi times the radius”, it was time to get cracking on the angle, Theta. In order to calculate that, I had to use the length of the two sides that I knew, which were ‘l’ and ‘r’, and then use arccosine to derive the angle. Since ‘l’ was the hypotenuse, it had to be the denominator, making ‘r’ the numerator. Once ‘r’ had been divided by ‘l’, the arccosine was applied to derive the angle. Since the distance per degree had already been calculated, all that had to be done was multiply it by the angle to get the ground distance. And Voila! Calculated. Here is the mathematical formula:
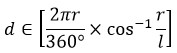
Once the known variables were applied to the formula, the calculations were easy:
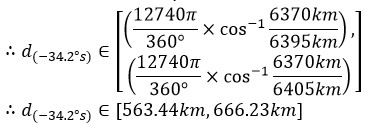
Now that I had the distance to the horizon, it was time to calculate at what time Golden Hour would occur over there. I looked up the definition of Golden Hour and this is what I found from www.timeanddate.com:
“Because the golden hour is a colloquial term, it doesn’t have an official definition similar to dawn, dusk, and the 3 phases of twilight. Rather, it refers to a state of natural lighting that is most common around sunrise and sunset.
However, the warm sunlight that is characteristic for the golden hour most likely occurs when the Sun is between 6 degrees below and 6 degrees above the horizon. By this definition, the golden hour begins with civil dawn in the morning and ends with civil dusk in the evening.”
Now that I knew that the sun had to be between 6° below and above the horizon, it was time to find out how to calculate that. Or so I thought.
I seems that the math needed to calculate was rather intensive and whatever I came up with would probably only be a fraction of a percentage more accurate than what is available online. Seeing as time was limited I headed over to www.timeanddate.com/sun/south-africa/port-elizabeth, and just looked up what time sunrise would take place in Port Elizabeth. I chose PE, because it is approximately 600km away from the estimated burst point.
I found that civil dawn would take place between 06h45 and 07h10 around the end of the month. In order to capture the sunrise, the balloon would have to be already near bursting altitude, as it would be the most stable. Since it takes around 1:40 hours to rise to bursting altitude, it would mean that I would have to launch at 05h15 in the morning in order to capture the sunrise.
Since the whole of today was used for something that was utterly useless, I had to come up with a plan for tomorrow. It is the first day I go back to school, so I will have to be ready for that. I will also need to build the parachute and test it, along with hacking the cameras and testing the camera life, as well as building the housing for the cameras and then also update the tracking software with my dad.
Although seemingly useless now, I’m sure that the calculations I did today will be useful for future launches, so it was not a total waste of time. But tomorrow I will have to be on top of my game, as time is truly of the essence.
[Image of Table Mountain taken by Johan Kok]





